Dinic 最大流

概述

dinic算法是网络流中的一种算法，这里拿来求最大流
所谓最大流就是一个网络中的最大流量，如下面这个图片

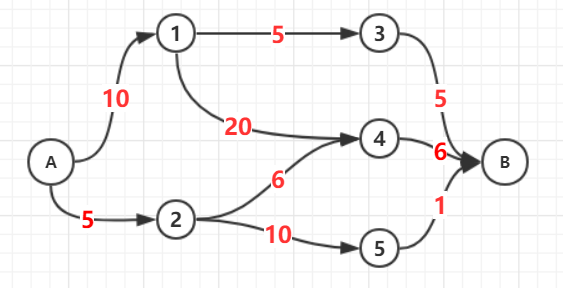
其中A称作源点，B称为汇点，边上的数字代表这条边最多能容纳多大的流量，所以上图的最大流量为12
dinic算法就是求最大流算法的一种

反向边概念

大部分网络流的算法都会在建边是建立一条反向边，初始权值为0，可以理解为给算法后悔的机会，在通过某条边流过流量时，将当前边的权值减去流过的流量，同时将其反向边加上流过的流量，可以理解为使算法将来有机会将多余的流量流回来，从而获得最终的最优解。权值修改后的图称之为残留图(通俗点就是新图)

链式前向星存图的小技巧

将边集数组的下标从0开始，每加一条边，就跟着加入它的反向边，这样后面访问的时候就可以用i^1来访问下标i这条边的反向边

分层图

分层图对与每个新图都要进行
dinic算法是在分层图上进行的，相比于EK算法，EK算法一次bfs可以找到一条可行的流量(增广路)，dinic在分层图上进行dfs，一次可以找到多条可行流量(增广路)，算法效率得到提升
将图分层是用bfs实现的

如上图，从A点开始bfs，A为第零层，从A一步可以到1和2结点，所以1，2属于第一层，一次类推，3，4，5属于第二层，B属于第四层。
分层的代码：

int bfs(int beg, int _end)
{
	queue<int>qu;
	qu.push(beg);
	memset(dfn, -1, sizeof(dfn));
	dfn[beg] = 0;//记录层次的数组
	while (!qu.empty())
	{
		int i;
		int tem = qu.front();
		qu.pop();
		for (i = head[tem]; i != -1; i = edge[i].next)
		{
			int v = edge[i]._end;
			if (dfn[v] != -1 || edge[i].w <= 0)continue;//该节点未访问过且到该节点的流量大于0
			dfn[v] = dfn[tem] + 1;//层次+1
			qu.push(v);
		}
	}
	return dfn[_end];//返回汇点所处于的层次。若汇点未被访问则代表当前的图中已经没有流量可以走了
}

分层的意义

在跑流量时，只往下层跑(即在分层图上dfs)。
同时一直在残留图上分层可以将这种情况给解决:

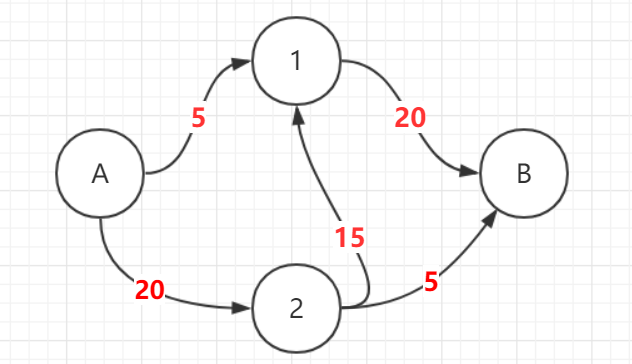
这个图中第一次分层时，1，2为同一层的结点，所以他们之间不会有流量经过，当A和1之间的流量跑完后，2就成了1上层的结点，所以在“一直在残留图上分层”这个前提下，优先将流量往下层跑是没错的。因为只用往下层跑，这样就加快了dfs的速度。

寻找增广路

在将图分层完成后，我们可以dfs来寻找增广路，dfs时只走dfn数组的值+1的点，也就是在分层上dfs
dfs的同时记录这条路上最狭窄的地方，用来更新边的权值

int dfs(int beg, int _end, int flow)//flow表示的是当前流过的流量
{
	int i;
	int ans = 0;
	if (beg == _end)
	{
		return flow;
	}
	for (i = head[beg]; i != -1; i = edge[i].next)
	{
		int v = edge[i]._end;
		if (dfn[v] != dfn[beg] + 1 || edge[i].w <= 0)continue;//只有是下一层的点且边权大于0才往下走
		int tmp = dfs(v, _end, min(flow - ans, edge[i].w));//flow-ans代表还剩余的流量
		ans += tmp;
		edge[i].w -= tmp;//更新边权
		edge[i ^ 1].w += tmp;//更新反向边的边权
	}
	if(!ans) dfn[beg]=-1;//这条边走不通
	return ans;
}

dinic

之后只要一边分层一边找增广路，直到图中没有可以从源点到汇点的流量
代码:

int dinic(int beg, int _end)
{
	int ans = 0;
	while (bfs(beg, _end) != -1)
	{
		ans += dfs(beg, _end, 0x7f7f7f7f);//初始给予一个无限大的流量
	}
	return ans;
}

例题 洛谷 P3367

代码:

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
typedef long long ll;
#define wfor(i,j,k) for(i=j;i<k;++i)
#define mfor(i,j,k) for(i=j;i>=k;--i)
// void read(int &x) {
// 	char ch = getchar(); x = 0;
// 	for (; ch < '0' || ch > '9'; ch = getchar());
// 	for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
// }
const int maxn = 2e5 + 5;
struct EDGE
{
	int first;
	int _end;
	int w;
	int next;
};
EDGE edge[maxn];
int head[maxn / 2];
int dft[maxn];
int cnt = -1;
void add(int beg, int _end, int w)
{
	edge[++cnt].next = head[beg];
	edge[cnt].first = beg;
	edge[cnt].w = w;
	edge[cnt]._end = _end;
	head[beg] = cnt;
}
int bfs(int beg, int _end)
{
	queue<int>qu;
	qu.push(beg);
	memset(dft, 0, sizeof(dft));
	dft[beg]=1;
	while (!qu.empty())
	{
		int temp = qu.front();
		qu.pop();
		for (int i = head[temp]; i != -1; i = edge[i].next)
		{
			int v = edge[i]._end;
			if (edge[i].w <= 0 || dft[v])
				continue;
            dft[v]=dft[temp]+1;
			qu.push(v);
		}
	}
	return dft[_end];
}
int dfs(int beg,int _end,int flow)
{
    if(beg==_end)
        return flow;
    int ans=0;
    for(int i=head[beg];i!=-1;i=edge[i].next)
    {
        int v=edge[i]._end;
        if(edge[i].w<=0) continue;
        if(dft[v]!=dft[beg]+1) continue;
        int temp=dfs(v,_end,min(edge[i].w,flow-ans));
        edge[i].w-=temp;
        edge[i^1].w+=temp;
        ans+=temp;
    }
    return ans;
}
int dinic(int beg,int _end)
{
    int ans=0;
    while(bfs(beg,_end))
    {
        ans+=dfs(beg,_end,0x7f7f7f7f);
    }
    return ans;
}
int main()
{
	std::ios::sync_with_stdio(false);
#ifdef test
	freopen("F:\\Desktop\\question\\in.txt", "r", stdin);
#endif
	int n, m, s, t;
	cin >> n >> m >> s >> t;
	int i;
	memset(head, -1, sizeof(head));
	wfor(i, 0, m)
	{
		int u, v, w;
		cin >> u >> v >> w;
		add(u, v, w);
		add(v, u, 0);
	}
	cout << dinic(s,t);
	return 0;
}