二分图匹配(匈牙利算法)

二分图的性质和一些名词

二分图的定义：一个图中的点可以分成两个不相交的集合\(A,B\)，并且图中所有的边都是从一个集合连向另一个集合，即同一个集合中的点之间没有边,如图1就是一个二分图

图1

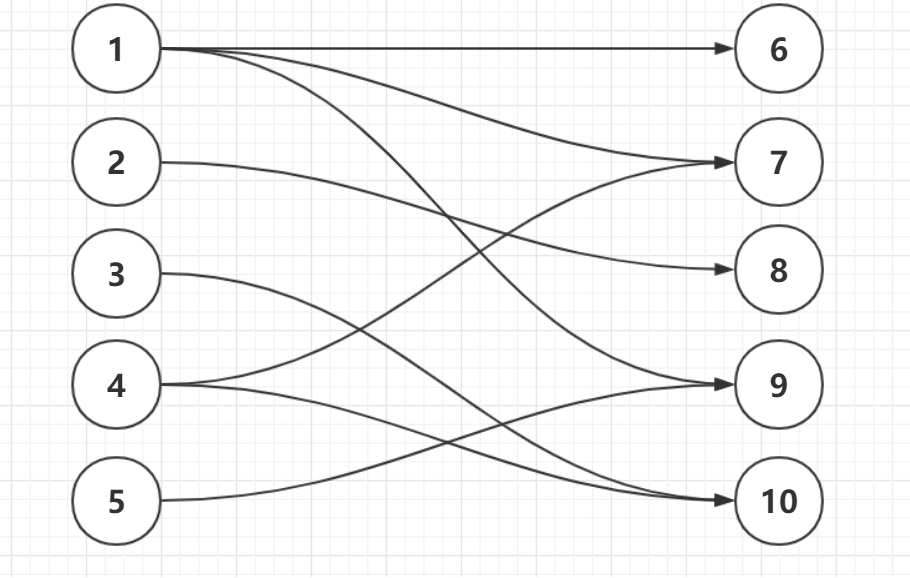
匹配:图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点，如图2中红色的边就是一个匹配

图2 **最大匹配**:一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配.

最大匹配数:最大匹配的匹配边的数目

最小点覆盖数:选取最少的点，使任意一条边至少有一个端点被选择

最大独立数:选取最多的点，使任意所选两点均不相连

最小路径覆盖数：给定有向图G=(V,E)。设P 是G 的一个简单路（顶点不相交）的集合。如果V 中每个顶点恰好在P 的一条路上，则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始，长度也是任意的，特别地，可以为0。G 的最小路径覆盖是G的所含路径条数最少的路径覆盖。

定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）

定理2：最大独立数=顶点数-最大匹配数

定理3：最小路径覆盖数 = 最小路径覆盖=|G|-最大匹配数
定理3中公式中最大匹配数是这样来的：
对于G中每一个节点x，建立节点x1，x2。若x- >y存在边，则x1与y2之间连一条无向边，求这个二分图的最大匹配数即可。

匈牙利算法中的一些定义

交替路:从一个为匹配点出发，循环经过匹配边，未匹配边的一条路称为交替路，如图3就是一条交替路，红色的边表示匹配边，红色的结点表示匹配点，非红色的表示未匹配的

图3 **增广路**:从一个未匹配点出发走到另一个未匹配的点，如上面的图3就是一条增广路。

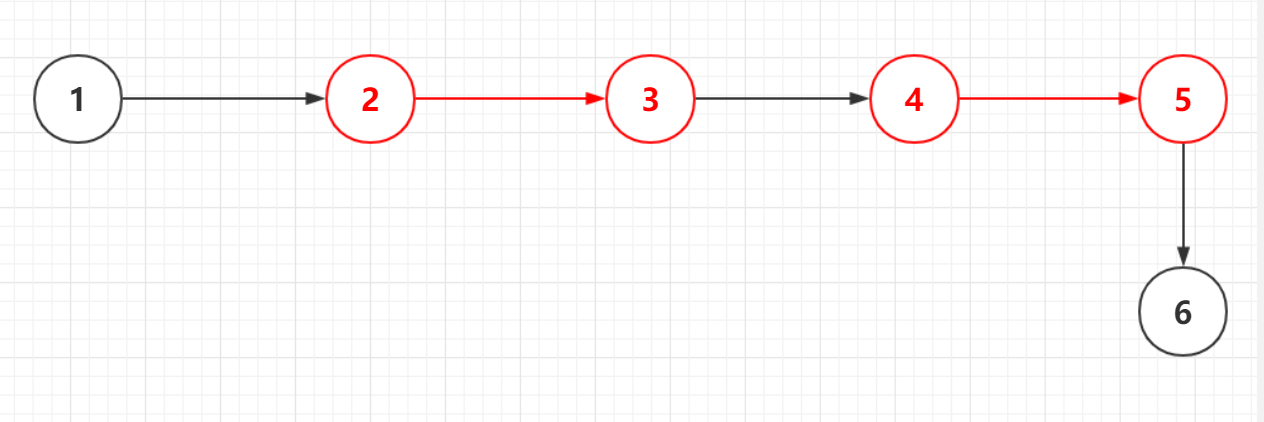
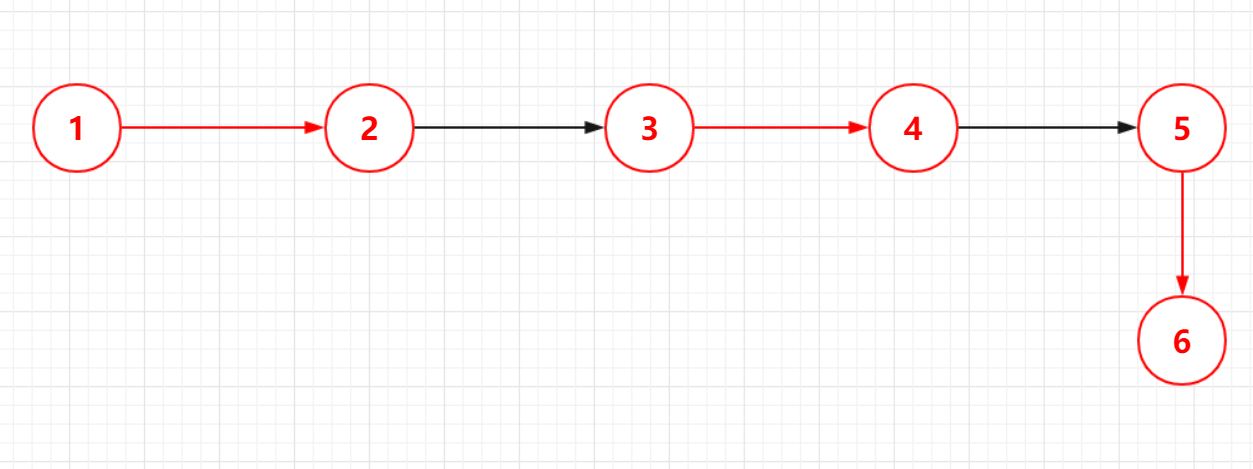
增广路的意义:如图3，未匹配边数为3，匹配边数为2，所有我们只需要将增广路的边的匹配状态与未匹配状态互换一下就可以多获得1个匹配边如图4，所有只需要不断得找增广路，并交换匹配状态直到找不到增广路，就可以得出最大匹配数

由图3交换边的匹配状态得来

DFS实现代码

#include <iostream>
#include <cstring> 
#include <cstdio>
using namespace std;
typedef long long ll;
#define wfor(i,j,k) for(i=j;i<k;++i)
#define mfor(i,j,k) for(i=j;i>=k;--i)
// void read(int &x) {
// 	char ch = getchar(); x = 0;
// 	for (; ch < '0' || ch > '9'; ch = getchar());
// 	for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
// }
const int maxn=10005;
struct st
{
    int end;
    int next;
};
st edge[maxn];
int head[maxn];
int cnt;
int ismaching[maxn];//该数组储存了相互匹配的点
int vis[maxn];
void add(int beg,int end)
{
    edge[++cnt].next=head[beg];
    edge[cnt].end=end;
    head[beg]=cnt;
}
int dfs(int beg)
{
    int i;
    for(i=head[beg];i;i=edge[i].next)
    {
        int v=edge[i].end;
        if(!vis[v])
        {
            vis[v]=1;
            if(ismaching[v]==-1||dfs(ismaching[v]))//找到未匹配的点
            {
                ismaching[beg]=v;//交换匹配与未匹配的边
                ismaching[v]=beg;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    std::ios::sync_with_stdio(false);
    #ifdef test
    freopen("F:\\Desktop\\question\\in.txt","r",stdin);
    #endif
    #ifdef ubuntu
    freopen("/home/time/debug/debug/in","r",stdin);
    freopen("/home/time/debug/debug/out","w",stdout);
    #endif
    int n,m,k;
    cin>>n>>m>>k;
    int i;
    wfor(i,0,k)
    {
        int u,v,id;
        cin>>id>>u>>v;
        add(u,v+n);
        add(v+n,u);
    }
    int ans=0;
    memset(ismaching,-1,sizeof(ismaching));
    wfor(i,1,n+1)
    {
        if(ismaching[i]==-1)//从未匹配的点开始
        {
            memset(vis,0,sizeof(vis));
            if(dfs(i)==1)//若找到增广路
                ans++;
        }
    }
    cout<<ans<<endl;
    return 0;
}