线段树

发表于 | 分类于 | 本文总阅读量 次

介绍

线段树的应用场景在区间修改和区间查询上，修改和查询的时间复杂度都为O(log n)
线段树如它的名字一样将区间分成一段一段的，如123456789这一串数字，以区间求和为例

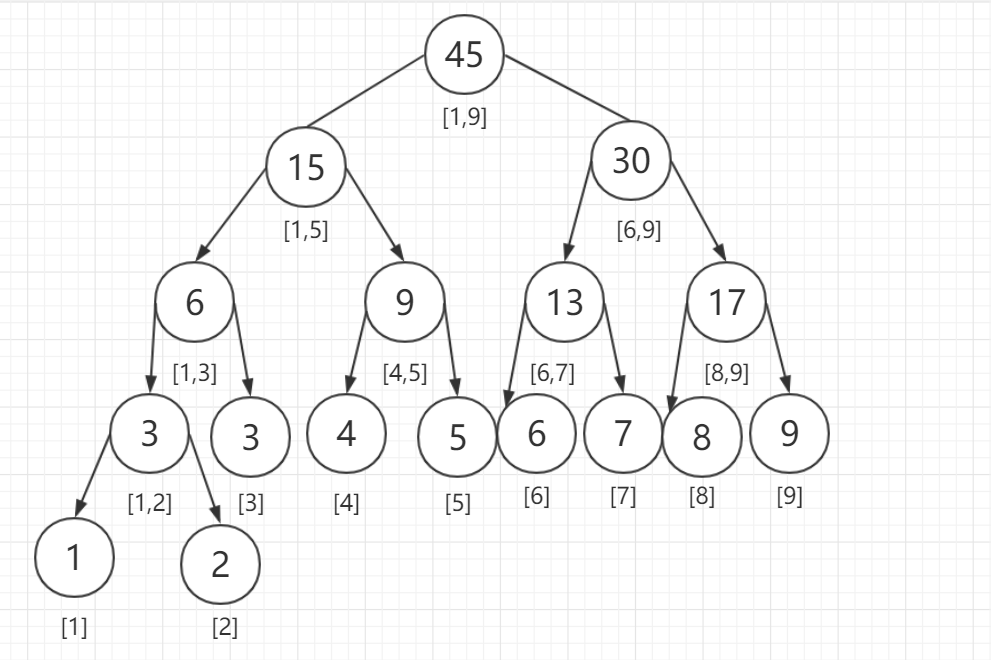
上图就是构建的线段树，其中结点里的值是该结点表示的区间的和，中括号里的数字代表表示的区间

实现(以区间求和为例)

定义

线段树的根结点定义为1，那么左子节点就是n*2，右子节点是n*+1
通常2*n在代码中写成 n<<1 。 2*n+1写成 n<<1|1 。
线段树所需的空间
足够的空间 = 数组大小n的四倍。
实际上足够的空间 = （n向上扩充到最近的2的某个次方）的两倍。

1
2
3
const int maxn = 100005;//元素的个数
ll tree[maxn << 2];//线段树的结点，大小开元素的4倍
ll add[maxn << 2];//标记数组(懒惰标记)区间修改会用到

建树

1
2
3
4
void push_up(int id)//根据子节点来更新父节点
{
    tree[id] = tree[id << 1] + tree[id << 1 | 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
void build(int l, int r, int id)//l,r表示当前区间，id表示当前结点的下标
{
    if (l == r)//到叶子结点就赋值
    {
        tree[id] = num[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(l, mid, id << 1);//递归构建左子树
    build(mid + 1, r, id << 1 | 1);//递归构建右子树
    push_up(id);//当前结点的子节点已经构建完成，然后更新当前结点
}

单点修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void update(int l, int r, int now, int number, int pos)
//l,r是当前区间，now是当前结点下标，number是要修改的数，pos是要修改的下标
{
    if (l == r)//到叶子结点直接修改
    {
        tree[now] += number;
        return ;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)//判断要修改的点在左子树还是右子树，然后递归修改
        update(l, mid, now << 1, number, pos);
    else
        update(mid + 1, r, now << 1 | 1, number, pos);
    push_up(now);//当前结点的子节点已经更新，所以更新当前结点
}

区间修改

关于区间的修改需要用到标记数组，改数组的含义是”当前结点的值已经更新，但是子节点的值未更新”
如add[7]=3,代表结点7的值已经更新，但是结点7的子节点都还没有加上这个值,这就需要一个下推标记的函数

1
2
3
4
5
6
7
8
9
10
11
12
void push_down(int id, int ln, int rn)
//id代表当前结点,ln代表左区间的元素个数，rn代表右区间的元素个数
{
    if (add[id] != 0)
    {
        tree[id << 1] += add[id] * ln;//更新左区间的值
        tree[id << 1 | 1] += add[id] * rn;//更新右区间的值
        add[id << 1] += add[id];//将标记下推，更新左区间标记
        add[id << 1 | 1] += add[id];//更新右区间标记
        add[id] = 0;//清空当前结点标记
    }
}

修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void update(int l, int r, int L, int R, int id, int number)
//l,r，id的含义不变，L，R代表需要修改的区间，number是要加上的数
{
    if (l >= L && r <= R)//若当前区间在需要修改的区间内，直接修改
    {
        tree[id] += number * (r - l + 1);
	//这里乘以区间长度是因为区间里的所有值都要加上number
        add[id] += number;//打上标记
        return ;
    }
    int mid = (l + r) >> 1;
    push_down(id, mid - l + 1, r - mid);//下推标记
    if (mid >= L)//若需要修改的区间与左区间相交，更新左区间
        update(l, mid, L, R, id << 1, number);
    if (mid < R)//若需要修改的区间与右区间相交，更新右区间
        update(mid + 1, r, L, R, id << 1 | 1, number);
    push_up(id);//当前结点的子节点已经更新，所以更新当前结点
}

查询

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int query(int l, int r, int L, int R, int id)//L,R是需要查询的区间
{
    if (l >= L && r <= R)//若当前区间在需要查询的区间内，直接返回值
    {
        return tree[id];
    }
    ll ans = 0;//累加答案
    int mid = (l + r) >> 1;
    push_down(id, mid - l + 1, r - mid);
    //可能更新中没有推完的标记，下推标记，如果只是单点修改这个可以不要
    if (mid >= L)//若需要查询的区间与左区间相交，查询左区间
        ans += query(l, mid, L, R, id << 1);
    if (mid < R)//若需要查询的区间与右区间相交，查询右区间
        ans += query(mid + 1, r, L, R, id << 1 | 1);
    return ans;
}

例题

HDU1166

单点修改的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
#define wfor(i,j,k) for(i=j;i<k;++i)
#define mfor(i,j,k) for(i=j;i>=k;--i)
// void read(int &x) {
//  char ch = getchar(); x = 0;
//  for (; ch < '0' || ch > '9'; ch = getchar());
//  for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
// }
const int maxn = 50005;
int tree[maxn << 2];
int num[maxn];
void push_up(int now)
{
    tree[now] = tree[now << 1] + tree[now << 1 | 1];
}
void build(int l, int r, int now)
{
    if (l == r)
    {
        tree[now] = num[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, now << 1);
    build(mid + 1, r, now << 1 | 1);
    push_up(now);
}
void update(int l, int r, int now, int number, int pos)
{
    if (l == r)
    {
        tree[now] += number;
        return ;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)
        update(l, mid, now << 1, number, pos);
    else
        update(mid + 1, r, now << 1 | 1, number, pos);
    push_up(now);
}
int query(int l, int r, int now, int L, int R)
{
    if (l >= L && r <= R)
    {
        return tree[now];
    }
    int ans = 0;
    int mid = (l + r) >> 1;
    if (mid >= L)
        ans += query(l, mid, now << 1, L, R);
    if (mid < R)
        ans += query(mid + 1, r, now << 1 | 1, L, R);
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
// #ifdef test
//     freopen("F:\\Desktop\\question\\in.txt", "r", stdin);
// #endif
// #ifdef ubuntu
//     freopen("/home/time/debug/debug/in", "r", stdin);
//     freopen("/home/time/debug/debug/out", "w", stdout);
// #endif
    int t;
    cin >> t;
    int casecnt = 0;
    while (t--)
    {
        casecnt++;
        cout << "Case " << casecnt << ":" << endl;
        int n;
        cin >> n;
        int i;
        wfor(i, 1, n + 1)
        {
            cin >> num[i];
        }
        build(1, n, 1);
        char op[10];
        while (cin >> op)
        {
            if (op[0] == 'A')
            {
                int number, pos;
                cin >> pos >> number;
                update(1, n, 1, number, pos);
            } else if (op[0] == 'S')
            {
                int number, pos;
                cin >> pos >> number;
                update(1, n, 1, -number, pos);
            } else if (op[0] == 'Q')
            {
                int l, r;
                cin >> l >> r;
                int ans = query(1, n, 1, l, r);
                cout << ans << endl;
            } else
            {
                break;
            }
        }
    }
    return 0;
}

POJ 3468

区间修改的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
#define wfor(i,j,k) for(i=j;i<k;++i)
#define mfor(i,j,k) for(i=j;i>=k;--i)
// void read(int &x) {
//  char ch = getchar(); x = 0;
//  for (; ch < '0' || ch > '9'; ch = getchar());
//  for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
// }
const int maxn = 100005;
int num[maxn];
ll tree[maxn << 2];
ll add[maxn << 2];
void push_up(int id)
{
    tree[id] = tree[id << 1] + tree[id << 1 | 1];
}
void build(int l, int r, int id)
{
    if (l == r)
    {
        tree[id] = num[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(l, mid, id << 1);
    build(mid + 1, r, id << 1 | 1);
    push_up(id);
}
void push_down(int id, int ln, int rn)
{
    if (add[id] != 0)
    {
        tree[id << 1] += add[id] * (ll)ln;
        tree[id << 1 | 1] += add[id] * (ll)rn;
        add[id << 1] += add[id];
        add[id << 1 | 1] += add[id];
        add[id] = 0;
    }
}
void update(int l, int r, int L, int R, int id, ll number)
{
    if (l >= L && r <= R)
    {
        tree[id] += number * (ll)(r - l + 1);
        add[id] += number;
        return ;
    }
    int mid = (l + r) >> 1;
    push_down(id, mid - l + 1, r - mid);
    if (mid >= L)
        update(l, mid, L, R, id << 1, number);
    if (mid < R)
        update(mid + 1, r, L, R, id << 1 | 1, number);
    push_up(id);
}
ll query(int l, int r, int L, int R, int id)
{
    if (l >= L && r <= R)
    {
        return tree[id];
    }
    ll ans = 0;
    int mid = (l + r) >> 1;
    push_down(id, mid - l + 1, r - mid);
    if (mid >= L)
        ans += query(l, mid, L, R, id << 1);
    if (mid < R)
        ans += query(mid + 1, r, L, R, id << 1 | 1);
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
// #ifdef test
//     freopen("F:\\Desktop\\question\\in.txt", "r", stdin);
// #endif
// #ifdef ubuntu
//     freopen("/home/time/debug/debug/in", "r", stdin);
//     freopen("/home/time/debug/debug/out", "w", stdout);
// #endif
    int n, q;
    cin >> n >> q;
    int i;
    wfor(i, 1, n + 1)
    {
        cin >> num[i];
    }
    build(1, n, 1);
    wfor(i, 0, q)
    {
        char op;
        cin >> op;
        if (op == 'Q')
        {
            int l, r;
            cin >> l >> r;
            ll ans = query(1, n, l, r, 1);
            cout << ans << endl;
        } else
        {
            int l, r;
            ll number;
            cin >> l >> r >> number;
            update(1, n, l, r, 1, number);
        }
    }
    return 0;
}

本文标题:线段树

文章作者:

发布时间:2019年04月21日 - 20:04

最后更新:2019年04月21日 - 22:04

原始链接:http://startcraft.cn/post/a7bbcc60.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

-------------The End-------------