线段树扫描线

发表于 | 分类于 | 本文总阅读量 次

矩形面积并

如图，考虑求图中矩形的面积并

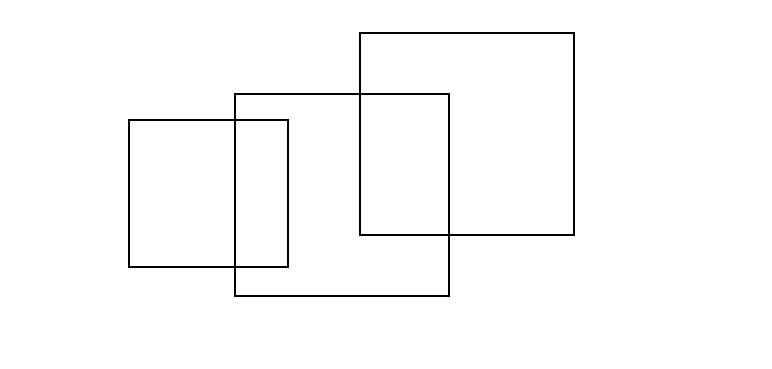
这个问题可以转换成求下图中这些部分的面积

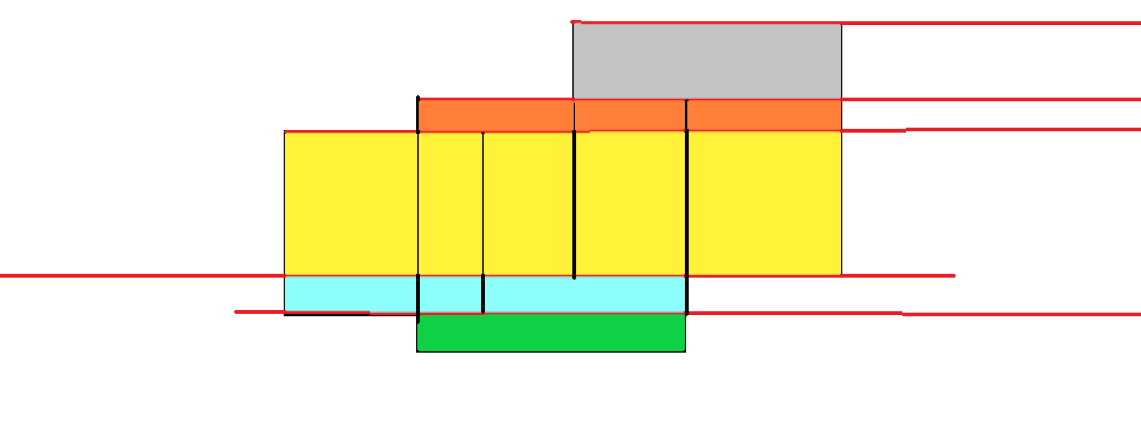
就是从下往上扫一遍，遇到矩形的下边就加入，然后统计当前的线段长度，当然重叠部分的线段只算一次长度，遇到上边就删除，然后每种颜色的矩形面积就是 当前线段长度(将要加入的线段的高度-上一条加入的线段的高度)*
然后这些累加起来就是矩形的面积并
现在的问题就是如何维护当前线段的长度
这里就要用到线段树了
先对矩形的边进行处理，按高度排序，然后下边标记为1，上边标记为-1，然后从下往上扫描
结点信息:

1
2
3
4
5
6
7
struct node
{
    int len;//当前区间的被覆盖的线段的长度
    int s;//当前区间被完全覆盖的次数
    int l;//当前区间的左端点
    int r;//当前区间的右端点
};

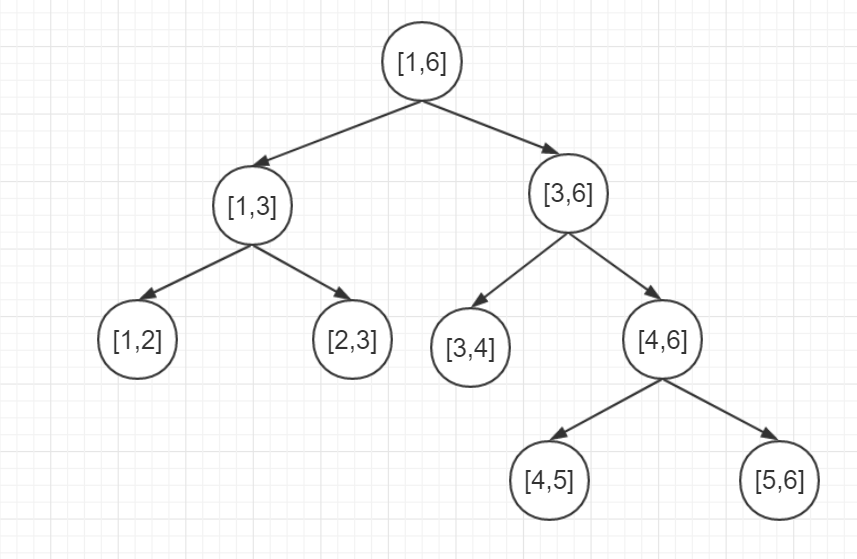
让后当前这个线段树的叶子结点是l+1==r，而不是传统的l==r，因为l==r是一个点这对矩形没有意义
构造线段树

1
2
3
4
5
6
7
8
9
10
11
12
void build (int l, int r, int id)
{
    tree[id].len = 0;
    tree[id].s = 0;
    tree[id].l = l;
    tree[id].r = r;
    if (l + 1 == r)//叶子结点
        return ;
    int mid = (l + r) >> 1;
    build(l, mid, id << 1);
    build(mid, r, id << 1 | 1);//不是mid+1,不然会导致一些区间无法覆盖
}

这样构造出来的线段树是长这样的

然后是push_up()函数

1
2
3
4
5
6
7
void push_up(int id)
{
    if (tree[id].s)//该区间被完全覆盖则长度就是区间的长度
        tree[id].len = r-l
    else//否则就是左区间的长度加右区间的长度
        tree[id].len = tree[id << 1].len + tree[id << 1 | 1].len;
}

有一点很重要，区间是否被完全覆盖是区间自己的事情，即不从子节点更新，也就是说[1,2],[2,3]被覆盖不代表[1,3]被覆盖，但是长度会从子节点更新，所以长度和被完全覆盖是一样的，答案不会错误，换句话说就是结点的s的值不从子节点更新，s的值只会在更新时被自己更新，所以虽然是区间更新，但与传统的区间更新有很大不同，也就不需要lazy tag和push_down
update

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void update(int id, int L, int R, int number)
{
    if (tree[id].l >= L && tree[id].r <= R)
    {
        tree[id].s += number;
	/*如果是下边就是1，代表该区间被完全覆盖了，如果是上边就是-1，覆盖次数就减了一次
	s的值不会小于0，因为下边总是先扫描到*/
        push_up(id);//计算当前区间的线段长度
        return ;
    }
    int mid = (tree[id].l + tree[id].r) >> 1;
    if (mid > L)
        update(id << 1, L, R, number);
    if (mid < R)
        update(id << 1 | 1, L, R, number);
    push_up(id);
}

查询的话，因为只需要知道总的线段的长度，所以只要tree[1].len

例题 HDU-1542

AC代码:这题的坐标有小数，所以需要离散化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <iostream>
#include <iomanip>
#include <vector>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;
#define wfor(i,j,k) for(i=j;i<k;++i)
#define mfor(i,j,k) for(i=j;i>=k;--i)
// void read(int &x) {
//  char ch = getchar(); x = 0;
//  for (; ch < '0' || ch > '9'; ch = getchar());
//  for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
// }
const int maxn = 2005;
struct node
{
    double len;
    int s;
    int l;
    int r;
};
node tree[maxn << 2];
struct Line
{
    int l;
    int r;
    int high;
    int flag;
    bool operator <(const Line other)const
    {
        return high < other.high;
    }
};
struct Point
{
    double x1;
    double y1;
    double x2;
    double y2;
};
Point point[maxn];
vector <double>num;
Line line[maxn << 2];
void push_up(int id)
{
    if (tree[id].s)
        tree[id].len = num[tree[id].r - 1] - num[tree[id].l - 1];
    else
        tree[id].len = tree[id << 1].len + tree[id << 1 | 1].len;
}
void build (int l, int r, int id)
{
    tree[id].len = 0;
    tree[id].s = 0;
    tree[id].l = l;
    tree[id].r = r;
    if (l + 1 == r)
    {
        return ;
    }
    int mid = (l + r) >> 1;
    build(l, mid, id << 1);
    build(mid, r, id << 1 | 1);
}
void update(int id, int L, int R, int number)
{
    if (tree[id].l >= L && tree[id].r <= R)
    {
        tree[id].s += number;
        push_up(id);
        return ;
    }
    int mid = (tree[id].l + tree[id].r) >> 1;
    if (mid > L)
        update(id << 1, L, R, number);
    if (mid < R)
        update(id << 1 | 1, L, R, number);
    push_up(id);
}
int main()
{
    std::ios::sync_with_stdio(false);
    int n;
    int casecnt = 0;
    while (cin >> n && n)
    {
        num.clear();
        casecnt++;
        int i;
        wfor(i, 0, n)
        {
            cin >> point[i].x1 >> point[i].y1 >> point[i].x2 >> point[i].y2;
            num.push_back(point[i].x1);
            num.push_back(point[i].x2);
            num.push_back(point[i].y1);
            num.push_back(point[i].y2);
        }
        sort(num.begin(), num.end());
        auto it = unique(num.begin(), num.end());
        int len = it - num.begin();
        int cnt = 0;
        wfor(i, 0, n)
        {
            int x1, y1, x2, y2;
            x1 = lower_bound(num.begin(), it, point[i].x1) - num.begin() + 1;
            x2 = lower_bound(num.begin(), it, point[i].x2) - num.begin() + 1;
            y1 = lower_bound(num.begin(), it, point[i].y1) - num.begin() + 1;
            y2 = lower_bound(num.begin(), it, point[i].y2) - num.begin() + 1;
            line[cnt].l = x1;
            line[cnt].r = x2;
            line[cnt].flag = 1;
            line[cnt++].high = y1;
            line[cnt].l = x1;
            line[cnt].r = x2;
            line[cnt].flag = -1;
            line[cnt++].high = y2;
        }
        sort(line, line + cnt);
        build(1, len, 1);
        update(1, line[0].l, line[0].r, line[0].flag);
        int last = line[0].high;
        double ans = 0;
        wfor(i, 1, cnt)
        {
            ans += tree[1].len * (num[line[i].high - 1] - num[last - 1]);
            update(1, line[i].l, line[i].r, line[i].flag);
            last = line[i].high;
        }
        cout << "Test case #" << casecnt << endl;
        cout << "Total explored area: ";
        cout << fixed << setprecision(2) << ans << endl;
        cout << endl;
    }
    return 0;
}

重叠矩形的周长

可以和计算面积一样的思路，对于所有的横边扫描一次，周长就是当前的线段长度与上一次的线段长度之差的绝对值
然后对竖着的边也做一次就是周长

例题 poj-1177

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;
#define wfor(i,j,k) for(i=j;i<k;++i)
#define mfor(i,j,k) for(i=j;i>=k;--i)
// void read(int &x) {
//  char ch = getchar(); x = 0;
//  for (; ch < '0' || ch > '9'; ch = getchar());
//  for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
// }
const int maxn = 20005;
struct node
{
    int l, r;
    int s;
    int len;
};
struct Line
{
    int l, r;
    int high;
    int flag;
    bool operator <(const Line & other)const
    {
        return high < other.high;
    }
};
vector <int>num;
struct Rect
{
    int x1;
    int y1;
    int x2;
    int y2;
};
Rect rec[maxn];
Line line1[maxn];
Line line2[maxn];
node tree[maxn << 2];
void build (int l, int r, int id)
{
    tree[id].l = l;
    tree[id].r = r;
    tree[id].len = 0;
    tree[id].s = 0;
    if (l + 1 == r)
        return ;
    int mid = (l + r) >> 1;
    build(l, mid, id << 1);
    build(mid, r, id << 1 | 1);
}
void push_up(int id)
{
    if (tree[id].s)
        tree[id].len = num[tree[id].r - 1] - num[tree[id].l - 1];
    else
        tree[id].len = tree[id << 1].len + tree[id << 1 | 1].len;
}
void update(int id, int L, int R, int number)
{
    if (tree[id].l >= L && tree[id].r <= R)
    {
        tree[id].s += number;
        push_up(id);
        return ;
    }
    int mid = (tree[id].l + tree[id].r) >> 1;
    if (mid > L)
        update(id << 1, L, R, number);
    if (mid < R)
        update(id << 1 | 1, L, R, number);
    push_up(id);
}
int main()
{
    std::ios::sync_with_stdio(false);
    int n;
    cin >> n;
    int i;
    wfor(i, 0, n)
    {
        cin >> rec[i].x1 >> rec[i].y1 >> rec[i].x2 >> rec[i].y2;
        num.push_back(rec[i].x1);
        num.push_back(rec[i].x2);
        num.push_back(rec[i].y1);
        num.push_back(rec[i].y2);
    }
    sort(num.begin(), num.end());
    vector<int>::iterator it = unique(num.begin(), num.end());
    int len = it - num.begin();
    int cnt = 0;
    wfor(i, 0, n)
    {
        rec[i].x1 = lower_bound(num.begin(), it, rec[i].x1) - num.begin() + 1;
        rec[i].x2 = lower_bound(num.begin(), it, rec[i].x2) - num.begin() + 1;
        rec[i].y1 = lower_bound(num.begin(), it, rec[i].y1) - num.begin() + 1;
        rec[i].y2 = lower_bound(num.begin(), it, rec[i].y2) - num.begin() + 1;
    }
    wfor(i, 0, n)
    {
        line1[cnt].l = rec[i].x1;
        line1[cnt].r = rec[i].x2;
        line1[cnt].high = rec[i].y1;
        line1[cnt].flag = 1;
        line2[cnt].l = rec[i].y1;
        line2[cnt].r = rec[i].y2;
        line2[cnt].high = rec[i].x1;
        line2[cnt++].flag = 1;
        line1[cnt].l = rec[i].x1;
        line1[cnt].r = rec[i].x2;
        line1[cnt].high = rec[i].y2;
        line1[cnt].flag = -1;
        line2[cnt].l = rec[i].y1;
        line2[cnt].r = rec[i].y2;
        line2[cnt].high = rec[i].x2;
        line2[cnt++].flag = -1;
    }
    sort(line1, line1 + cnt);
    sort(line2, line2 + cnt);
    ll ans = 0;
    build(1, len, 1);
    update(1, line1[0].l, line1[0].r, line1[0].flag);
    ans += num[line1[0].r - 1] - num[line1[0].l - 1];
    int last = ans;
    wfor(i, 1, cnt)
    {
        update(1, line1[i].l, line1[i].r, line1[i].flag);
        ans += abs(tree[1].len - last);
        last = tree[1].len;
    }
    build(1, len, 1);
    update(1, line2[0].l, line2[0].r, line2[0].flag);
    ans += num[line2[0].r - 1] - num[line2[0].l - 1];
    last = num[line2[0].r - 1] - num[line2[0].l - 1];
    wfor(i, 1, cnt)
    {
        update(1, line2[i].l, line2[i].r, line2[i].flag);
        ans += abs(tree[1].len - last);
        last = tree[1].len;
    }
    cout << ans << endl;
    return 0;
}

本文标题:线段树扫描线

文章作者:

发布时间:2019年05月29日 - 12:05

最后更新:2019年05月29日 - 15:05

原始链接:http://startcraft.cn/post/dbbb0af0.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

-------------The End-------------