题目链接 https://nanti.jisuanke.com/t/41420

题目大意

给你一些石头,让你选一些石头重量大于剩余的重量,且去掉任意一个你选的石头之后总重量小于等于剩余重量

思路

将石头按从大到小排序,然后遍历选取，以当前的石头为最小值,也就是当前的石头一定要选,比它大的可选可不选,比它小的一定不选
然后就是背包问题了,dp[j]代表选择石头的总重量为j的方案数,判断一下j合不合法,合法就加上dp[j-num[i]];

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6567

题目大意

给你两棵树，让你在两棵树之间加一条边,使得两棵树联通且任意两结点之间的距离之和最短
就是最小化这个式子
$$
\sum_{i=1}^n\sum_{j=i+1}^ndis\left(i,j\right)
$$

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6570

题目大意:

给你长度为N,$1\leq N\leq100000$的一个数组，其中元素在$[1,c] 1\leq c\leq 100$之内，求一个最长的子序列满足奇数位数字都相同，偶数位数字也都相同,但是奇偶位之间不同，问你子序列的长度

题目链接:https://ac.nowcoder.com/acm/contest/882/F

题目大意:

有2N个人，任意两个人之间有一个竞争值，将这2N个人分成两组，每组N个人，只有在不同组的两人之间才计算他们的竞争值，问可以获得的最大竞争值是多少。$ 1\leq N \leq 14 $

矩形面积并

如图，考虑求图中矩形的面积并

这个问题可以转换成求下图中这些部分的面积

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1540

题目大意:

一些村庄排成一排，编号1-N,只要中间没有被摧毁的村庄，两个村庄就算是连接在一起的，现在有三个操作
1.摧毁编号为X的村庄
2.询问与村庄X连接的村庄有几个
3.重建上一个被摧毁的村庄

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4027

题目大意:

给你一个初始序列a[i],然后有两个操作，一个是询问区间的和，一个是将区间里的每一个数变为原来的平方根，向下取整。操作数<=100000

思路

给定的数初始最大为\(2^{63}\),那么我们最多取6次平方根就可以将其变为1，变成1之后不管怎么取都是1，所以考虑使用线段树维护一个区间最大值，当最大值为1时这个区间就不用计算了，不为1时就暴力递归更新结点的值。
因为取平方根的次数很少所以暴力递归更新的次数也很少不会超时。
不知道线段树的可以看看我之前写的线段树入门:https://startcraft.cn/post/a7bbcc60.html#more
https://blog.csdn.net/lalala445566/article/details/89440830
该题有一个坑点，数据给的区间可能l>r

ST表概述

ST是解决区间RMQ(区间最值)问题的一种数据结构，它不支持在线修改，预处理\(O(nlogn)\),查询\(O(1)\)

实现

以区间最小值为例子

预处理

\(ans[i][j]\)表示区间\([i,i+2^{j}-1]\)的最小值，同时它可以表示成前半个区间的最小值和后半个区间的最小值
前半个区间是\([i,i+2^{j-1}-1]\),可以表示成\(ans[i][j-1]\)，那么后半个区间是\([i+2^{j-1},i+2^{j}-1]\),可以表示成\(ans[i+2^{j-1}][j-1]\)
即
$$
ans[i][j]=min(ans[i][j-1],ans[i+2^{j-1}][j-1])
$$
所以初始化的时间复杂度是\(O(nlogn)\)

介绍

线段树的应用场景在区间修改和区间查询上，修改和查询的时间复杂度都为O(log n)
线段树如它的名字一样将区间分成一段一段的，如123456789这一串数字，以区间求和为例

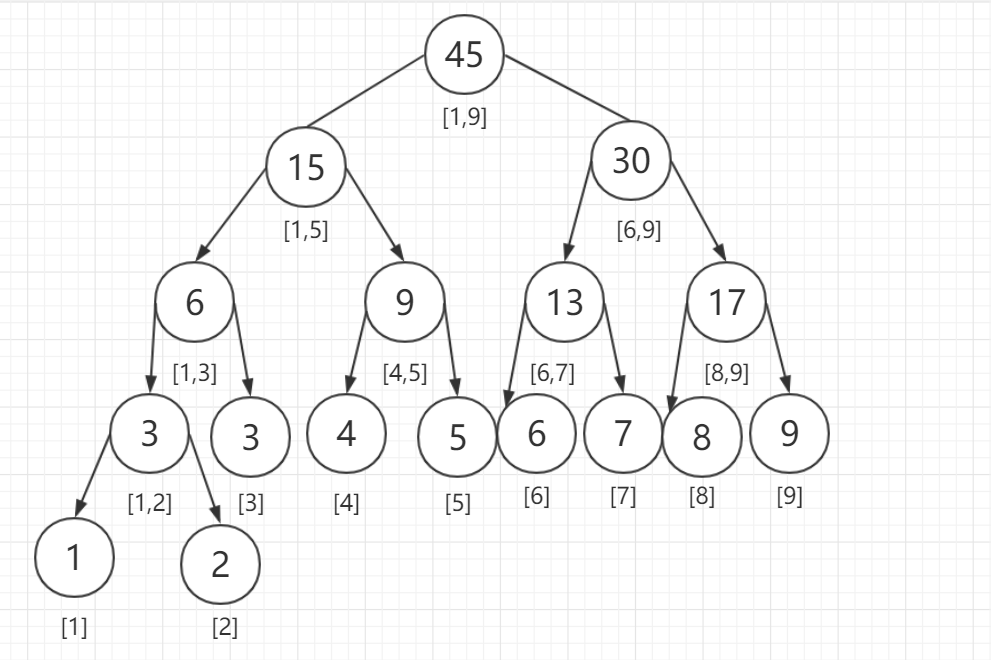
上图就是构建的线段树，其中结点里的值是该结点表示的区间的和，中括号里的数字代表表示的区间

题目链接:https://codeforces.com/gym/101981/attachments

Given a suqence of n integers \(a_{i}\)
Let \(mul(l, r)\) = \(\prod ^{r}_{i=1}\)and\(fac(l,r)\)be the number of distinct prime factors of\(mul(l,r)\).
Please calculate \(\sum ^{n}_{i=1}\sum ^{n}_{j=1}fac(i,j)\)

Input
The first line contains one integer \(n (1\leq n\leq 10^{6})\)— the length of the sequence.
The second line contains n integers \(a_{i} (1\leq a_{i}\leq 10^{6})\)—the sequence.
Output
Print the answer to the equation.